Unit T Big Question #4

Why do sine and cosine not have asymptotes, but the other four trig graphs do?

Sin's ratio in the Unit Circle is "y" over "r". Cos's ratio in the Unit Circle is "x" over "r". Because the trig graphs are directly related to the Unit Circle, sin and cos do not have asymptotes because their ratios do not allow them to. "R" in the Unit Circle, is always 1. Asymptotes exist when there is a zero in the denominator, making it undefined. This cannot be possible for sin and cos because their ratios will never have zero in the denominator. Csc, sec, tan, and cot, however, have asymptotes because their ratios do not have "r" as the denominator so therefore they can have a zero in the denominator.

Unit T Big Question #3

Why is a "normal" tangent graph uphill, but a "normal" tangent graph downhill.

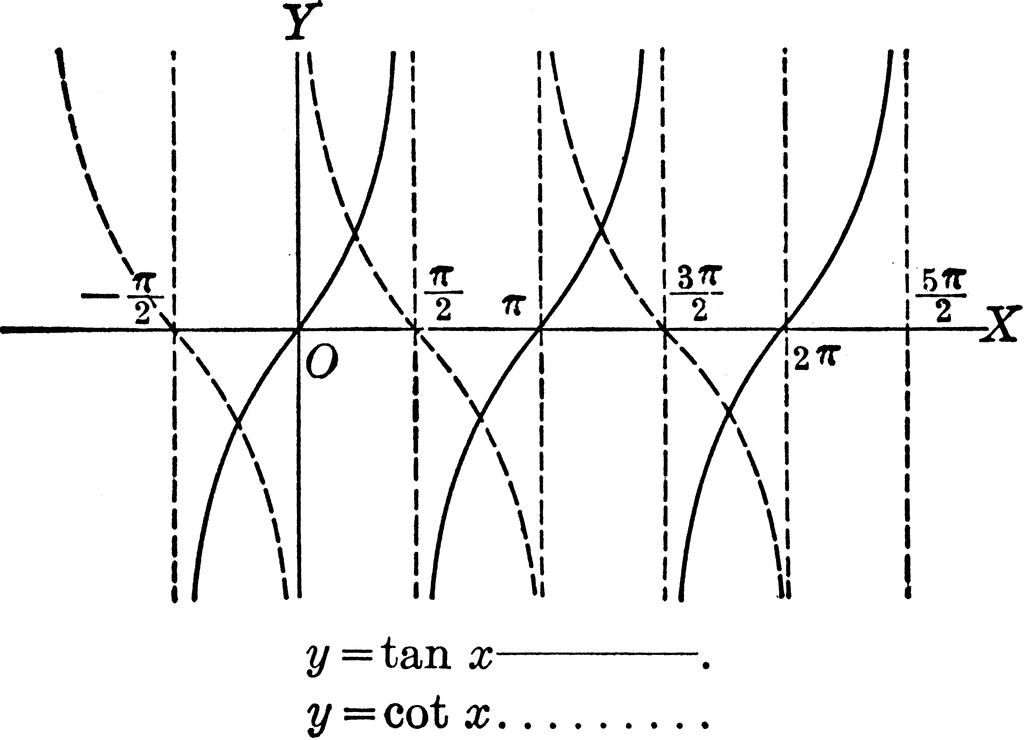
This has to do with the Unit Circle, ASTC, and the ratios for tangent and cotangent. The ratio for tangent is sin over cosine while the ratio for cotangent is cosine over sine.For tangent, this means that whenever cosine is zero, there will be an asymptote because it is the denominator. For cotangent, this means that whenever sine is zero, there will be an asymptote because it is the denominator. In the Unit Circle, cosine is zero at 90 degrees (pi/2) and 270 degrees (3pi/2) and sine is zero at 0 degrees (0 radians) and at 180 degrees (pi). This means that there will be asymptotes at pi over 2 and at 3pi over 2 for the tangent graph; 0 and pi for the cotangent graph. ASTC will cause the tangent graph to go uphill and the cotangent graph to go downhill because of where the asymptotes are placed.

Unit T Big Question #2

How do the graphs of sine and cosine relate to each of the others?

Sin and cos graphs do not relate at all to the tangent and cotangent graphs. They are complete opposites. sine and cosine do not have asymptotes like tangent and cotangent. Tangent and cotangent do not use the sine and cosine graphs as references like the secant and cosecant  do. Sine and cosine's domains are all real numbers while tangent and cotangent's are limited. Tangent and cotangent's ranges are all real numbers while sine and cosine's are limited. Sin and cosines have amplitudes while tangent and cotangent do not. Sine and cosine have periods of 2pi while tangent and cotangent have periods of pi.

Secant and cosecant graphs, however, are directly related to sine and cosine graphs. Secant and cosecant graphs' shapes are based on their corresponding cosine and sine graphs. Secant and csc use sin and cos's amplitudes to plot certain points. Sec and csc use the x-intercepts of sin and cos's to draw out their asymptotes. Without these asymptotes, a sec or csc graph cannot be drawn.

Unit T Big Question #1

The Unit Circle has four quadrants, each separated by half of pi (Quadrant I: 0 to pi over 2, Quadrant II: pi over 2 to pi, Quadrant III: pi to 3pi over 2, Quadrant IV: 3pi over 2 to 2pi). The trig graphs' x-axis is separated also by these values. The trig graphs' x-axis is just the unit circle values in a linear perspective.

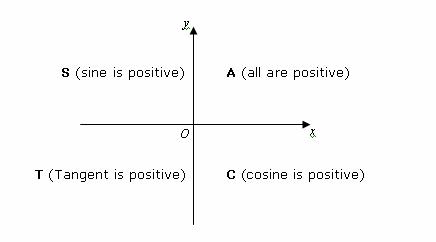
 Whether a trig function is positive or negative in a certain quadrant (ASTC) is determined in the Unit Circle and this dictates how we draw the trig graphs. If the trig function value is positive, we draw it above the x-axis; below if it is negative.

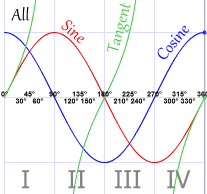
Sin is positive in the first quadrant and the second quadrant; it is negative in the third and the fourth. If one goes counterclockwise, starting from quadrant 1, one will see that this pattern continues after the first rotation which is 2pi. Cosine has a similar pattern that repeats itself after 2pi. Tangent's ASTC pattern is: postive in the 1st, negative in the second, positive in the 3rd and negative in the fourth. This pattern, as you can see, repeats itself after the second quadrant which is represented by pi. Cotangent has the same pattern as tangent.

Unit S Assessment 4

This problem is about trigonometric equations that we have to solve using the half angle formulas we learned earlier in this unit. By substituting in a trigonometric half-angle formula for a certain expression, we can then use algebra, the unit circle, and the trig identities to simplify the new equation.

Pay special attention to the caution I practiced when I started a new step for every thing I did. I did this so that it would be less likely for me to make a mistake.

Unit S Assessment 2

Although the final answers from the half angle expressions are different than their difference formula counterparts, they are the same value. If you plug in the trig functions in a calculator for 75 degrees, you will get about .966 for sine, about .259 for cosine, and about 3.732 for tangent. When I plug in the expressions carefully and correctly, I get the exact same answers. If you check and get different answers, are you sure your calculator is in degrees and not in radians?

Unit S Assessment 3

This problem is about simplifying trigonometric expressions using power-reducing formulas. For the problem I simplified above, I had to use the sine and cosine power reducing formulas because tangent was irrelevant. 

Pay special attention to the formulas and the way I kept simplifying them. If the formula is off or if you make a mistake simplifying then your final answer can be wrong.