To have the most successful year possible in this class you must do your work! Do all the work that is assigned, do it on time, and do it to improve your mastery of the concepts and to be prepared for the tests. If I did all the work assigned, I would now have a near perfect grade. If I did all the work on time, I would not have so many homework cards, central detentions and Saturday schools like I do now. If I did not do the work (the PQ's/PT's), then I would not be as confident as I am now for calculus. Do your work; that's all you need to do.
There is no best way to adjust to the flipped classroom. You just do it. Think about adjusting to the flipped classroom as an obstacle that you must overcome in order to succeed in this class. Do what Mrs. Kirch says. Trust her. I know there is a lot of work that seems pointless or sometimes degrading but if you want to pass this class with an A then just do it because you will thank Mrs. Kirch later for getting you well prepared for calculus which is the point of this class.
There is not much difference from the previous math classes. You learn a concept and then you do a lot of problems to practice your understanding of the concept. The only differences will be that you will use technology a lot more and where you learn the concept and where you do the problems are switched.
Thursday, June 6, 2013
Monday, June 3, 2013
Unit V Big Question
Where does the formula for the difference quotient come from?
The difference quotient formula is:
f(x + h) - f(x) / h
H is also known as delta x.
In a graph, one can find a secant of the graph by using two points and finding the slope of this secant. One point would be (x, f(x)). The second x-value would be delta x units away which would make the second point (x + delta x, f(x + delta x)). Using the slope formula: y2 - y1 / x2 - x1 we would get the difference quotient if you substitute delta x for h and if you combine like terms correctly you would get the difference quotient formula above. However, one would only get the slope of a secant formula but to ensure one gets the slope of the tangent line, one must place a limit and more specifically a limit that has h approaching 0.
The difference quotient formula is:
f(x + h) - f(x) / h
H is also known as delta x.
In a graph, one can find a secant of the graph by using two points and finding the slope of this secant. One point would be (x, f(x)). The second x-value would be delta x units away which would make the second point (x + delta x, f(x + delta x)). Using the slope formula: y2 - y1 / x2 - x1 we would get the difference quotient if you substitute delta x for h and if you combine like terms correctly you would get the difference quotient formula above. However, one would only get the slope of a secant formula but to ensure one gets the slope of the tangent line, one must place a limit and more specifically a limit that has h approaching 0.
Tuesday, May 28, 2013
Unit U Big Questions
1) What is continuity? What is discontinuity?
Continuity is when you can draw a graph without lifting your pencil from the paper; it has no breaks in it.
Discontinuity is when there are breaks in the graph and cannot be drawn without lifting your pencil from the paper.
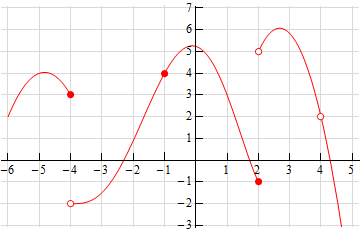
2) What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?
A limit is the intended height of a function. A limit exists when the value of the limit is the same from both the left side and the right side like it does in the function in the left below at x equals 1. A limit does not exist when the value of the left side and the right side are different or cannot be reached like in the function on the left below at x equals negative 1 or in the function in the right below at x equals 2. A limit is the intended height of a function while a value is the height the function actually reaches like in the function on the left below where the limit at x equals 1 is 2 but the value is actually 3.
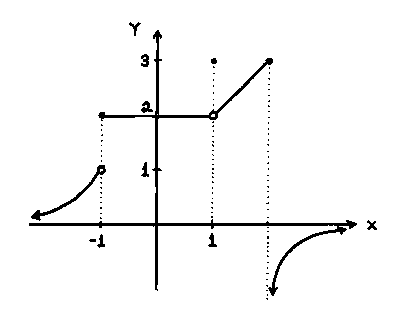
3) How do we evaluate limits numerically, graphically, and algebraically?
Numerically, we evaluate limits using a table by making our best guess what the limit would be if we used x values that are close to the limit we approach.
Graphically, we evaluate limits by checking from the left and the right what the limit is.
Algebraically, we evaluate limits by doing direct substitution, factoring, or rationalizing.
Continuity is when you can draw a graph without lifting your pencil from the paper; it has no breaks in it.
Discontinuity is when there are breaks in the graph and cannot be drawn without lifting your pencil from the paper.
2) What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?
A limit is the intended height of a function. A limit exists when the value of the limit is the same from both the left side and the right side like it does in the function in the left below at x equals 1. A limit does not exist when the value of the left side and the right side are different or cannot be reached like in the function on the left below at x equals negative 1 or in the function in the right below at x equals 2. A limit is the intended height of a function while a value is the height the function actually reaches like in the function on the left below where the limit at x equals 1 is 2 but the value is actually 3.
3) How do we evaluate limits numerically, graphically, and algebraically?
Numerically, we evaluate limits using a table by making our best guess what the limit would be if we used x values that are close to the limit we approach.
Graphically, we evaluate limits by checking from the left and the right what the limit is.
Algebraically, we evaluate limits by doing direct substitution, factoring, or rationalizing.
Wednesday, April 24, 2013
Unit T Big Question #4
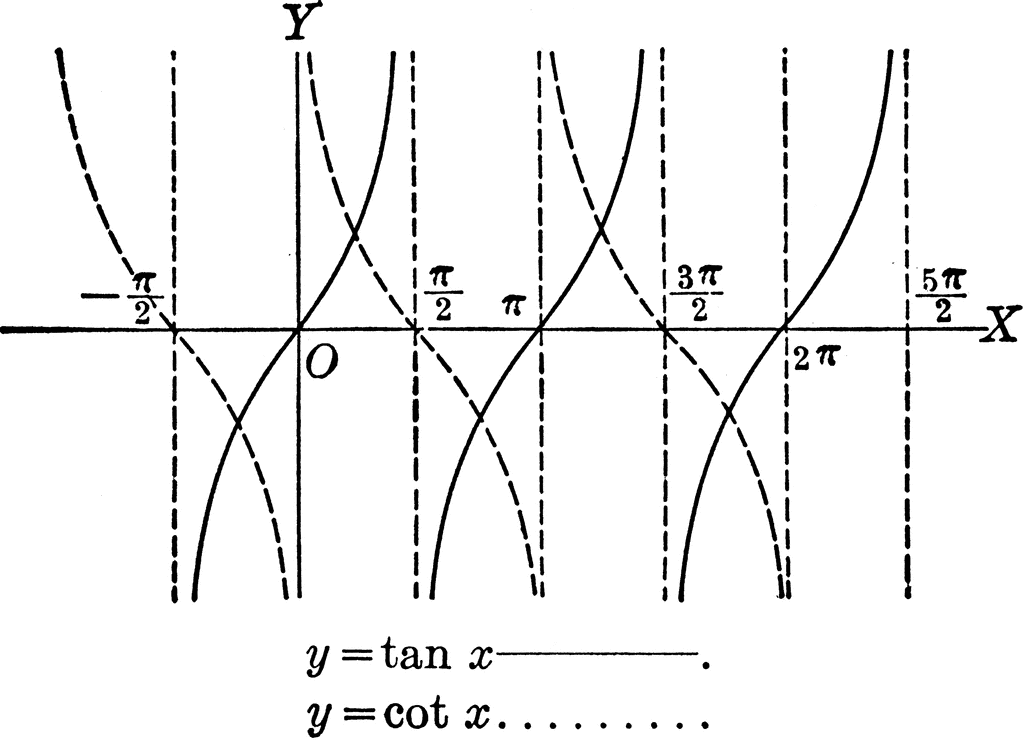
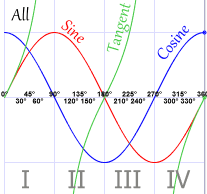
Why do sine and cosine not have asymptotes, but the other four trig graphs do?
Sin's ratio in the Unit Circle is "y" over "r". Cos's ratio in the Unit Circle is "x" over "r". Because the trig graphs are directly related to the Unit Circle, sin and cos do not have asymptotes because their ratios do not allow them to. "R" in the Unit Circle, is always 1. Asymptotes exist when there is a zero in the denominator, making it undefined. This cannot be possible for sin and cos because their ratios will never have zero in the denominator. Csc, sec, tan, and cot, however, have asymptotes because their ratios do not have "r" as the denominator so therefore they can have a zero in the denominator.
Sin's ratio in the Unit Circle is "y" over "r". Cos's ratio in the Unit Circle is "x" over "r". Because the trig graphs are directly related to the Unit Circle, sin and cos do not have asymptotes because their ratios do not allow them to. "R" in the Unit Circle, is always 1. Asymptotes exist when there is a zero in the denominator, making it undefined. This cannot be possible for sin and cos because their ratios will never have zero in the denominator. Csc, sec, tan, and cot, however, have asymptotes because their ratios do not have "r" as the denominator so therefore they can have a zero in the denominator.
Unit T Big Question #3
Why is a "normal" tangent graph uphill, but a "normal" tangent graph downhill.
This has to do with the Unit Circle, ASTC, and the ratios for tangent and cotangent. The ratio for tangent is sin over cosine while the ratio for cotangent is cosine over sine.For tangent, this means that whenever cosine is zero, there will be an asymptote because it is the denominator. For cotangent, this means that whenever sine is zero, there will be an asymptote because it is the denominator. In the Unit Circle, cosine is zero at 90 degrees (pi/2) and 270 degrees (3pi/2) and sine is zero at 0 degrees (0 radians) and at 180 degrees (pi). This means that there will be asymptotes at pi over 2 and at 3pi over 2 for the tangent graph; 0 and pi for the cotangent graph. ASTC will cause the tangent graph to go uphill and the cotangent graph to go downhill because of where the asymptotes are placed.
This has to do with the Unit Circle, ASTC, and the ratios for tangent and cotangent. The ratio for tangent is sin over cosine while the ratio for cotangent is cosine over sine.For tangent, this means that whenever cosine is zero, there will be an asymptote because it is the denominator. For cotangent, this means that whenever sine is zero, there will be an asymptote because it is the denominator. In the Unit Circle, cosine is zero at 90 degrees (pi/2) and 270 degrees (3pi/2) and sine is zero at 0 degrees (0 radians) and at 180 degrees (pi). This means that there will be asymptotes at pi over 2 and at 3pi over 2 for the tangent graph; 0 and pi for the cotangent graph. ASTC will cause the tangent graph to go uphill and the cotangent graph to go downhill because of where the asymptotes are placed.
Unit T Big Question #2
How do the graphs of sine and cosine relate to each of the others?
Sin and cos graphs do not relate at all to the tangent and cotangent graphs. They are complete opposites. sine and cosine do not have asymptotes like tangent and cotangent. Tangent and cotangent do not use the sine and cosine graphs as references like the secant and cosecant do. Sine and cosine's domains are all real numbers while tangent and cotangent's are limited. Tangent and cotangent's ranges are all real numbers while sine and cosine's are limited. Sin and cosines have amplitudes while tangent and cotangent do not. Sine and cosine have periods of 2pi while tangent and cotangent have periods of pi.
Secant and cosecant graphs, however, are directly related to sine and cosine graphs. Secant and cosecant graphs' shapes are based on their corresponding cosine and sine graphs. Secant and csc use sin and cos's amplitudes to plot certain points. Sec and csc use the x-intercepts of sin and cos's to draw out their asymptotes. Without these asymptotes, a sec or csc graph cannot be drawn.
Unit T Big Question #1
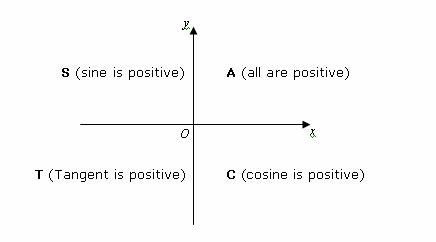
The Unit Circle has four quadrants, each separated by half of pi (Quadrant I: 0 to pi over 2, Quadrant II: pi over 2 to pi, Quadrant III: pi to 3pi over 2, Quadrant IV: 3pi over 2 to 2pi). The trig graphs' x-axis is separated also by these values. The trig graphs' x-axis is just the unit circle values in a linear perspective.
Whether a trig function is positive or negative in a certain quadrant (ASTC) is determined in the Unit Circle and this dictates how we draw the trig graphs. If the trig function value is positive, we draw it above the x-axis; below if it is negative.
Sin is positive in the first quadrant and the second quadrant; it is negative in the third and the fourth. If one goes counterclockwise, starting from quadrant 1, one will see that this pattern continues after the first rotation which is 2pi. Cosine has a similar pattern that repeats itself after 2pi. Tangent's ASTC pattern is: postive in the 1st, negative in the second, positive in the 3rd and negative in the fourth. This pattern, as you can see, repeats itself after the second quadrant which is represented by pi. Cotangent has the same pattern as tangent.
Sin is positive in the first quadrant and the second quadrant; it is negative in the third and the fourth. If one goes counterclockwise, starting from quadrant 1, one will see that this pattern continues after the first rotation which is 2pi. Cosine has a similar pattern that repeats itself after 2pi. Tangent's ASTC pattern is: postive in the 1st, negative in the second, positive in the 3rd and negative in the fourth. This pattern, as you can see, repeats itself after the second quadrant which is represented by pi. Cotangent has the same pattern as tangent.
Sunday, April 14, 2013
Unit S Assessment 4
This problem is about trigonometric equations that we have to solve using the half angle formulas we learned earlier in this unit. By substituting in a trigonometric half-angle formula for a certain expression, we can then use algebra, the unit circle, and the trig identities to simplify the new equation.
Pay special attention to the caution I practiced when I started a new step for every thing I did. I did this so that it would be less likely for me to make a mistake.
Unit S Assessment 2
Unit S Assessment 3
This problem is about simplifying trigonometric expressions using power-reducing formulas. For the problem I simplified above, I had to use the sine and cosine power reducing formulas because tangent was irrelevant.
Pay special attention to the formulas and the way I kept simplifying them. If the formula is off or if you make a mistake simplifying then your final answer can be wrong.
Wednesday, March 27, 2013
Unit R Concept 3 - Student Problem
This problem is about finding the trig function of an inverse trig function. The "type 2" problem I made and solved above comprises of using Unit Circle values to easily find the trig function values inside the parenthesis.
Pay close attention to the fact that I used the 1st quadrant angle for sin v = 0 instead of the 2nd quadrant angle. If I chose the second one then the answer will be different but it would not be necessarily wrong.
Tuesday, March 26, 2013
Unit R Concept 2 - Student Problem
This problem is about using the sum and difference formulas. Only this time it is when values are given for a right triangle.
Pay close attention to the way I drew the triangles with the knowledge of which quadrants they were in. The way you draw the triangles is crucial to finding the desired and unknown trig functions.
Monday, March 25, 2013
Unit R Concept 1 - Student Problem
This problem is about using the sum and difference formulas of the 3 main trig functions. These formulas help us find the exact values of angles that are not apart of the magic five reference angles (0,30,45,60,90) by adding or subtracting two of the angles given in the unit circle to get the desired angle.
Pay close attention to the order of the variables and how I first found the exact values of cos,sin, and tan of the two angles. The order of the variables is crucial for one to obtain the correct answer when using certain formulas. The finding of the exact values helped me accelerate my finding of the exact values of the trig functions of the desired angle.
Wednesday, March 20, 2013
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
Saturday, March 16, 2013
Math Analysis Reflective Blog Post
1. How have you performed on the Unit O and P tests? What evidence do you have from your work in the unit that supports your test grade (good or bad)? Be specific and include a minimum of three pieces of evidence.
I performed a little below my expectations, I got 89 on my Unit P test and 83 on my Unit O test. I expected myself to achieve at least an A (95) for both. I did not do any form of practice for the review which is why I am not surprised I did bad. I did exceptionally well on the concept's 1-3 part of the Unit P test which was the easiest one which is supported by the PQ's and PT's that I completed and checked for that part. There was one question from the Concept's 1-3 section of the Unit O test that I did completely wrong. I think that one was a concept 3 question and I just noticed that I did not do PQ's or PT's for that one. I also got the Concept 6 question wrong for the Unit P test and I did not do the PQ's nor the PTs for that concept.For Unit O, I did horribly on the concept 7-8 portion of the test because I did not do the PQ's nor the PT's for that concept as well. For the review portion of the Unit O test I did uncharacteristically bad (I always get 10/10 but I got 3/10 this time). I did not do any form of practice for the review which is why I am not surprised I did bad.I did do well with everything else of the Unit O test which is supported by all the PQ's and PT's i did for them.
2. You are able to learn material in a variety of ways in Math Analysis. It generally follows this pattern:
→ Your initial source of information is generally the video lessons and SSS packets followed by a processing and reflection activity via the WSQ
→ individual supplemental research online or in the textbook before class
→ reviewing and accessing supplementary resources provided by Mrs. Kirch on the blog
→ discussion with classmates about key concepts
→ practice of math concepts through PQs
→ formatively assessing your progress through concept quizzes
→ cumulatively reviewing material through PTs
→ Final Assessment via Unit Test.
Talk through each of the steps given in the following terms:
a. How seriously do you take this step for your learning? What evidence do you have to support your claim? Make sure to make reference to all 8 steps.
b. How could you improve your focus and attention on this step to improve your mastery of the material? What specific next steps would this entail? Make sure to make reference to all 8 steps.
a) I take the WSQ videos and the WSQ submission very seriously. I make sure I complete this assignment before I do the rest of my homework plus I rarely miss a WSQ submission. I do not take the individual research online or in the textbook very seriously. How do I know this? I forgot that I have a math textbook until right now that I am typing this.I rarely review and access supplementary resources that Mrs. Kirch provides because I usually understand the concept and have no need for this step.As of recently, I have been trying to discuss key concepts with classmates. James Pham, Hieu Nguyen, and I have used our seminar teacher's (Mr. Muniz) whiteboard to practice key concepts like deriving the law of cosines and stuff like that. I take completing PQs very seriously. If I do not do these than I only have basic knowledge and little practice for the consolidation of my understanding of the concept. I take somewhat serious the quizzes. If I get 8's or 5's then I am good with that and I forget about the concept but if I get a 2 on a certain quiz then I take note of that and I try to do better with the PTs. I take completing PTs somewhat serious as well. If I do well on the PQ's and the quizzes then I do not make sure that the PT's are done to the best of my ability. It depends on what I receive as my grade and what concepts I messed up in on the severity of my Unit Test. If I get an A then I know I did well and no longer have to worry about mastering the unit. If I get a lower grade than an A and it was because of small mistakes then I do not worry to much of this.
b) I do not know how I could improve my focus and attention to the videos and WSQ submissions. I rarely do bad on this. For the individual research, I could actually start doing this. I could take the step of immediately looking up additional information on the internet or in my textbook after the WSQ video is over. Again I could start doing the reviewing and accessing of the resources provided by Mrs. Kirch. I could immediately access these after doing my individual research and then I could review them before the test. I do not think I could improve on discussing with classmates about key concepts (Mr. Muniz's whiteboard markers are getting dry). I do not think I could improve on the PQ's either. I should take the quizzes more seriously and start focusing on the concepts that I do not get an 8. I will review the research I did individually and the research Mrs. Kirch provided. I do not think I have to improve my focus and attention of reviewing through PTs but if I did, I would do all of the PT's quickly and to the best of my ability so that I will be ready for the concepts I did not do well on the quizzes. I could take the Unit Test's more seriously by doing all of the above and correcting them on my own time after I get it back.
3. Reflect on your learning this year thus far by considering the following questions:
a. How confident do you generally feel on the day of a Unit Test? Give evidence and specifics to back up your answer.
b. How well do you feel you have learned the math material this year as compared to your previous years in math? Give evidence to support your claim.
c. How DEEPLY do you feel you have learned the math material this year as compared to your previous years in math? Give evidence to support your claim.
d. Do you normally feel like you understand the WHY behind the math and not just the WHAT/HOW? Meaning, do you understand why things work, how they are connected to each other, etc, and not just the procedures? Explain your answer in detail and cite specific evidence from this year.
e. How does your work ethic relate to your performance and success? What is the value of work ethic in real life?
a) I do not feel anything on the day of a Unit Test. I just go inside the classroom and take the test. To support this I would say that I usually forget that there is a test the day of the test until someone asks me if I am ready for it.
b) I feel I learned the math material as well as I have in my previous years of math. Like in the years before this one, I would learn a concept thoroughly but instead of through a million problems like in Algebra 1, Geometry and Algebra 2, I learn it through videos and half a million problems and making my own videos for the concept. Then the concept fades away until i remember it in a new math problem or test.
c) I do not feel anything about the math material I learned this year as compared to my previous year in math. Evidence = :l
d) Yes I usually understand the Why and not just the What/How. Sometimes I do not understand the why, which is the reason I ask it in a Hot Question the day after I watch the video. The law of cosines, for example, was a concept I did not know why it was true until you told us why in class one day.
e) My performance and success has nothing to do with my work ethic in math. I feel i do not try as hard as I do in my other classes when I am in math. I rarely study for math but I get my best grades there yet I study my hardest for my APChem and APUSH classes but i get my worst grades there. If someone is not successful, usually it is because of laziness. Work ethic is what gets you noticed and rewarded in real life. Drew Brees, the quarterback for the New Orleans Saints, has an outstanding work ethic. He spends most of his time practicing and preparing and planning for a football game. I heard that he even calls his teammates and coaches in the middle of the night asking a question about a certain play or making sure that they are in the same page or just talking about a new idea he got for a play on gameday. He is considered an elite quarterback and it shows by his statistics that he achieved through his respected work ethic. Work ethic is key to success.
I performed a little below my expectations, I got 89 on my Unit P test and 83 on my Unit O test. I expected myself to achieve at least an A (95) for both. I did not do any form of practice for the review which is why I am not surprised I did bad. I did exceptionally well on the concept's 1-3 part of the Unit P test which was the easiest one which is supported by the PQ's and PT's that I completed and checked for that part. There was one question from the Concept's 1-3 section of the Unit O test that I did completely wrong. I think that one was a concept 3 question and I just noticed that I did not do PQ's or PT's for that one. I also got the Concept 6 question wrong for the Unit P test and I did not do the PQ's nor the PTs for that concept.For Unit O, I did horribly on the concept 7-8 portion of the test because I did not do the PQ's nor the PT's for that concept as well. For the review portion of the Unit O test I did uncharacteristically bad (I always get 10/10 but I got 3/10 this time). I did not do any form of practice for the review which is why I am not surprised I did bad.I did do well with everything else of the Unit O test which is supported by all the PQ's and PT's i did for them.
2. You are able to learn material in a variety of ways in Math Analysis. It generally follows this pattern:
→ Your initial source of information is generally the video lessons and SSS packets followed by a processing and reflection activity via the WSQ
→ individual supplemental research online or in the textbook before class
→ reviewing and accessing supplementary resources provided by Mrs. Kirch on the blog
→ discussion with classmates about key concepts
→ practice of math concepts through PQs
→ formatively assessing your progress through concept quizzes
→ cumulatively reviewing material through PTs
→ Final Assessment via Unit Test.
Talk through each of the steps given in the following terms:
a. How seriously do you take this step for your learning? What evidence do you have to support your claim? Make sure to make reference to all 8 steps.
b. How could you improve your focus and attention on this step to improve your mastery of the material? What specific next steps would this entail? Make sure to make reference to all 8 steps.
a) I take the WSQ videos and the WSQ submission very seriously. I make sure I complete this assignment before I do the rest of my homework plus I rarely miss a WSQ submission. I do not take the individual research online or in the textbook very seriously. How do I know this? I forgot that I have a math textbook until right now that I am typing this.I rarely review and access supplementary resources that Mrs. Kirch provides because I usually understand the concept and have no need for this step.As of recently, I have been trying to discuss key concepts with classmates. James Pham, Hieu Nguyen, and I have used our seminar teacher's (Mr. Muniz) whiteboard to practice key concepts like deriving the law of cosines and stuff like that. I take completing PQs very seriously. If I do not do these than I only have basic knowledge and little practice for the consolidation of my understanding of the concept. I take somewhat serious the quizzes. If I get 8's or 5's then I am good with that and I forget about the concept but if I get a 2 on a certain quiz then I take note of that and I try to do better with the PTs. I take completing PTs somewhat serious as well. If I do well on the PQ's and the quizzes then I do not make sure that the PT's are done to the best of my ability. It depends on what I receive as my grade and what concepts I messed up in on the severity of my Unit Test. If I get an A then I know I did well and no longer have to worry about mastering the unit. If I get a lower grade than an A and it was because of small mistakes then I do not worry to much of this.
b) I do not know how I could improve my focus and attention to the videos and WSQ submissions. I rarely do bad on this. For the individual research, I could actually start doing this. I could take the step of immediately looking up additional information on the internet or in my textbook after the WSQ video is over. Again I could start doing the reviewing and accessing of the resources provided by Mrs. Kirch. I could immediately access these after doing my individual research and then I could review them before the test. I do not think I could improve on discussing with classmates about key concepts (Mr. Muniz's whiteboard markers are getting dry). I do not think I could improve on the PQ's either. I should take the quizzes more seriously and start focusing on the concepts that I do not get an 8. I will review the research I did individually and the research Mrs. Kirch provided. I do not think I have to improve my focus and attention of reviewing through PTs but if I did, I would do all of the PT's quickly and to the best of my ability so that I will be ready for the concepts I did not do well on the quizzes. I could take the Unit Test's more seriously by doing all of the above and correcting them on my own time after I get it back.
3. Reflect on your learning this year thus far by considering the following questions:
a. How confident do you generally feel on the day of a Unit Test? Give evidence and specifics to back up your answer.
b. How well do you feel you have learned the math material this year as compared to your previous years in math? Give evidence to support your claim.
c. How DEEPLY do you feel you have learned the math material this year as compared to your previous years in math? Give evidence to support your claim.
d. Do you normally feel like you understand the WHY behind the math and not just the WHAT/HOW? Meaning, do you understand why things work, how they are connected to each other, etc, and not just the procedures? Explain your answer in detail and cite specific evidence from this year.
e. How does your work ethic relate to your performance and success? What is the value of work ethic in real life?
a) I do not feel anything on the day of a Unit Test. I just go inside the classroom and take the test. To support this I would say that I usually forget that there is a test the day of the test until someone asks me if I am ready for it.
b) I feel I learned the math material as well as I have in my previous years of math. Like in the years before this one, I would learn a concept thoroughly but instead of through a million problems like in Algebra 1, Geometry and Algebra 2, I learn it through videos and half a million problems and making my own videos for the concept. Then the concept fades away until i remember it in a new math problem or test.
c) I do not feel anything about the math material I learned this year as compared to my previous year in math. Evidence = :l
d) Yes I usually understand the Why and not just the What/How. Sometimes I do not understand the why, which is the reason I ask it in a Hot Question the day after I watch the video. The law of cosines, for example, was a concept I did not know why it was true until you told us why in class one day.
e) My performance and success has nothing to do with my work ethic in math. I feel i do not try as hard as I do in my other classes when I am in math. I rarely study for math but I get my best grades there yet I study my hardest for my APChem and APUSH classes but i get my worst grades there. If someone is not successful, usually it is because of laziness. Work ethic is what gets you noticed and rewarded in real life. Drew Brees, the quarterback for the New Orleans Saints, has an outstanding work ethic. He spends most of his time practicing and preparing and planning for a football game. I heard that he even calls his teammates and coaches in the middle of the night asking a question about a certain play or making sure that they are in the same page or just talking about a new idea he got for a play on gameday. He is considered an elite quarterback and it shows by his statistics that he achieved through his respected work ethic. Work ethic is key to success.
Thursday, March 7, 2013
Monday, February 25, 2013
Subscribe to:
Posts (Atom)