To have the most successful year possible in this class you must do your work! Do all the work that is assigned, do it on time, and do it to improve your mastery of the concepts and to be prepared for the tests. If I did all the work assigned, I would now have a near perfect grade. If I did all the work on time, I would not have so many homework cards, central detentions and Saturday schools like I do now. If I did not do the work (the PQ's/PT's), then I would not be as confident as I am now for calculus. Do your work; that's all you need to do.
There is no best way to adjust to the flipped classroom. You just do it. Think about adjusting to the flipped classroom as an obstacle that you must overcome in order to succeed in this class. Do what Mrs. Kirch says. Trust her. I know there is a lot of work that seems pointless or sometimes degrading but if you want to pass this class with an A then just do it because you will thank Mrs. Kirch later for getting you well prepared for calculus which is the point of this class.
There is not much difference from the previous math classes. You learn a concept and then you do a lot of problems to practice your understanding of the concept. The only differences will be that you will use technology a lot more and where you learn the concept and where you do the problems are switched.
Thursday, June 6, 2013
Monday, June 3, 2013
Unit V Big Question
Where does the formula for the difference quotient come from?
The difference quotient formula is:
f(x + h) - f(x) / h
H is also known as delta x.
In a graph, one can find a secant of the graph by using two points and finding the slope of this secant. One point would be (x, f(x)). The second x-value would be delta x units away which would make the second point (x + delta x, f(x + delta x)). Using the slope formula: y2 - y1 / x2 - x1 we would get the difference quotient if you substitute delta x for h and if you combine like terms correctly you would get the difference quotient formula above. However, one would only get the slope of a secant formula but to ensure one gets the slope of the tangent line, one must place a limit and more specifically a limit that has h approaching 0.
The difference quotient formula is:
f(x + h) - f(x) / h
H is also known as delta x.
In a graph, one can find a secant of the graph by using two points and finding the slope of this secant. One point would be (x, f(x)). The second x-value would be delta x units away which would make the second point (x + delta x, f(x + delta x)). Using the slope formula: y2 - y1 / x2 - x1 we would get the difference quotient if you substitute delta x for h and if you combine like terms correctly you would get the difference quotient formula above. However, one would only get the slope of a secant formula but to ensure one gets the slope of the tangent line, one must place a limit and more specifically a limit that has h approaching 0.
Tuesday, May 28, 2013
Unit U Big Questions
1) What is continuity? What is discontinuity?
Continuity is when you can draw a graph without lifting your pencil from the paper; it has no breaks in it.
Discontinuity is when there are breaks in the graph and cannot be drawn without lifting your pencil from the paper.
2) What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?
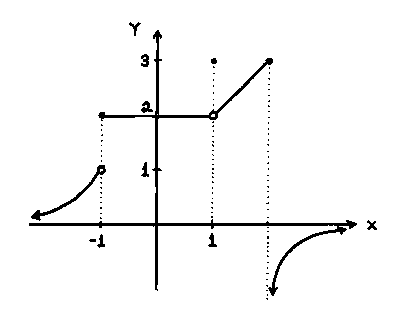
A limit is the intended height of a function. A limit exists when the value of the limit is the same from both the left side and the right side like it does in the function in the left below at x equals 1. A limit does not exist when the value of the left side and the right side are different or cannot be reached like in the function on the left below at x equals negative 1 or in the function in the right below at x equals 2. A limit is the intended height of a function while a value is the height the function actually reaches like in the function on the left below where the limit at x equals 1 is 2 but the value is actually 3.
3) How do we evaluate limits numerically, graphically, and algebraically?
Numerically, we evaluate limits using a table by making our best guess what the limit would be if we used x values that are close to the limit we approach.
Graphically, we evaluate limits by checking from the left and the right what the limit is.
Algebraically, we evaluate limits by doing direct substitution, factoring, or rationalizing.
Continuity is when you can draw a graph without lifting your pencil from the paper; it has no breaks in it.
Discontinuity is when there are breaks in the graph and cannot be drawn without lifting your pencil from the paper.
2) What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?
A limit is the intended height of a function. A limit exists when the value of the limit is the same from both the left side and the right side like it does in the function in the left below at x equals 1. A limit does not exist when the value of the left side and the right side are different or cannot be reached like in the function on the left below at x equals negative 1 or in the function in the right below at x equals 2. A limit is the intended height of a function while a value is the height the function actually reaches like in the function on the left below where the limit at x equals 1 is 2 but the value is actually 3.
3) How do we evaluate limits numerically, graphically, and algebraically?
Numerically, we evaluate limits using a table by making our best guess what the limit would be if we used x values that are close to the limit we approach.
Graphically, we evaluate limits by checking from the left and the right what the limit is.
Algebraically, we evaluate limits by doing direct substitution, factoring, or rationalizing.
Wednesday, April 24, 2013
Unit T Big Question #4
Why do sine and cosine not have asymptotes, but the other four trig graphs do?
Sin's ratio in the Unit Circle is "y" over "r". Cos's ratio in the Unit Circle is "x" over "r". Because the trig graphs are directly related to the Unit Circle, sin and cos do not have asymptotes because their ratios do not allow them to. "R" in the Unit Circle, is always 1. Asymptotes exist when there is a zero in the denominator, making it undefined. This cannot be possible for sin and cos because their ratios will never have zero in the denominator. Csc, sec, tan, and cot, however, have asymptotes because their ratios do not have "r" as the denominator so therefore they can have a zero in the denominator.
Sin's ratio in the Unit Circle is "y" over "r". Cos's ratio in the Unit Circle is "x" over "r". Because the trig graphs are directly related to the Unit Circle, sin and cos do not have asymptotes because their ratios do not allow them to. "R" in the Unit Circle, is always 1. Asymptotes exist when there is a zero in the denominator, making it undefined. This cannot be possible for sin and cos because their ratios will never have zero in the denominator. Csc, sec, tan, and cot, however, have asymptotes because their ratios do not have "r" as the denominator so therefore they can have a zero in the denominator.
Unit T Big Question #3
Why is a "normal" tangent graph uphill, but a "normal" tangent graph downhill.
This has to do with the Unit Circle, ASTC, and the ratios for tangent and cotangent. The ratio for tangent is sin over cosine while the ratio for cotangent is cosine over sine.For tangent, this means that whenever cosine is zero, there will be an asymptote because it is the denominator. For cotangent, this means that whenever sine is zero, there will be an asymptote because it is the denominator. In the Unit Circle, cosine is zero at 90 degrees (pi/2) and 270 degrees (3pi/2) and sine is zero at 0 degrees (0 radians) and at 180 degrees (pi). This means that there will be asymptotes at pi over 2 and at 3pi over 2 for the tangent graph; 0 and pi for the cotangent graph. ASTC will cause the tangent graph to go uphill and the cotangent graph to go downhill because of where the asymptotes are placed.
This has to do with the Unit Circle, ASTC, and the ratios for tangent and cotangent. The ratio for tangent is sin over cosine while the ratio for cotangent is cosine over sine.For tangent, this means that whenever cosine is zero, there will be an asymptote because it is the denominator. For cotangent, this means that whenever sine is zero, there will be an asymptote because it is the denominator. In the Unit Circle, cosine is zero at 90 degrees (pi/2) and 270 degrees (3pi/2) and sine is zero at 0 degrees (0 radians) and at 180 degrees (pi). This means that there will be asymptotes at pi over 2 and at 3pi over 2 for the tangent graph; 0 and pi for the cotangent graph. ASTC will cause the tangent graph to go uphill and the cotangent graph to go downhill because of where the asymptotes are placed.
Unit T Big Question #2
How do the graphs of sine and cosine relate to each of the others?
Sin and cos graphs do not relate at all to the tangent and cotangent graphs. They are complete opposites. sine and cosine do not have asymptotes like tangent and cotangent. Tangent and cotangent do not use the sine and cosine graphs as references like the secant and cosecant do. Sine and cosine's domains are all real numbers while tangent and cotangent's are limited. Tangent and cotangent's ranges are all real numbers while sine and cosine's are limited. Sin and cosines have amplitudes while tangent and cotangent do not. Sine and cosine have periods of 2pi while tangent and cotangent have periods of pi.
Secant and cosecant graphs, however, are directly related to sine and cosine graphs. Secant and cosecant graphs' shapes are based on their corresponding cosine and sine graphs. Secant and csc use sin and cos's amplitudes to plot certain points. Sec and csc use the x-intercepts of sin and cos's to draw out their asymptotes. Without these asymptotes, a sec or csc graph cannot be drawn.
Unit T Big Question #1
The Unit Circle has four quadrants, each separated by half of pi (Quadrant I: 0 to pi over 2, Quadrant II: pi over 2 to pi, Quadrant III: pi to 3pi over 2, Quadrant IV: 3pi over 2 to 2pi). The trig graphs' x-axis is separated also by these values. The trig graphs' x-axis is just the unit circle values in a linear perspective.
Whether a trig function is positive or negative in a certain quadrant (ASTC) is determined in the Unit Circle and this dictates how we draw the trig graphs. If the trig function value is positive, we draw it above the x-axis; below if it is negative.
Sin is positive in the first quadrant and the second quadrant; it is negative in the third and the fourth. If one goes counterclockwise, starting from quadrant 1, one will see that this pattern continues after the first rotation which is 2pi. Cosine has a similar pattern that repeats itself after 2pi. Tangent's ASTC pattern is: postive in the 1st, negative in the second, positive in the 3rd and negative in the fourth. This pattern, as you can see, repeats itself after the second quadrant which is represented by pi. Cotangent has the same pattern as tangent.
Sin is positive in the first quadrant and the second quadrant; it is negative in the third and the fourth. If one goes counterclockwise, starting from quadrant 1, one will see that this pattern continues after the first rotation which is 2pi. Cosine has a similar pattern that repeats itself after 2pi. Tangent's ASTC pattern is: postive in the 1st, negative in the second, positive in the 3rd and negative in the fourth. This pattern, as you can see, repeats itself after the second quadrant which is represented by pi. Cotangent has the same pattern as tangent.
Subscribe to:
Posts (Atom)