Fibonacci Haiku

Music.
 Electro.
DJs, composers.
Their energy inspires.
Producers make fun, original songs.
The sexy beats; the cool rhythm blows minds.

WPP 10

Create your own Playlist on MentorMob!

WPP #9

Create your own Playlist on MentorMob!

WPP #7

Create your own Playlist on MentorMob!

Student Problem #4

This is a graph of a logarithmic function where the function, its key points, its (horizontal) asymptote, its x-intercept, its y-intercept, its domain, and its range is shown. Pay special attention to the range, it is infinite both ways which is the exact opposite of exponential functions where their domain is infinite both ways.

Student Problem #3

This is a graph of an exponential function where the function, its key points, its asymptote, its x-intercept, it y-intercept, its domain and its range is shown. Pay close attention to the function and be aware that h is the opposite of what it is because even though it says "x-2", h is actually positive 2. Also be aware of the fact that there is no x-intercept because 1) you get an undefined answer when solving for it and 2) the graph will not hit the x-axis because the vertical asymptote will not allow it.

Student Problem #6

This is an example of a partial fraction decomposition with repeated factors. You do the exact same thing as the PFD with distinct factors except that when you start, the factors that are repeated will be separated into separate fractions. You count up the powers and include the factors as many times as the exponent number.

Student Problem #5

This is picture shows my example of solving a partial fraction decomposition with distinct factors. To solve a partial fraction decomposition with distinct factors problem, first you have to factor the denominator if possible or if not already done (x * x+1 * x-1). Then for each factor, use a letter beginning with A as your numerator and the factor as your denominator (A/x, B/x+1, C/x-1). Next, you have to add these new fractions with each other (A/x + B/x+1 + C/x-1) and set it equal to the original fraction. Now you would need the same denominator to go any further so multiply each fraction with whats missing and you will get like terms. Simplify these like terms and turn it into a system. Solve the system and the substitute the answers with the letters of the fraction.

Student Problem #2

This video shows my boy Jonathan and myself solving a logarithmic problem that we created. This type of problem is found in our Unit H SSS packet and more specifically in the "finding logs given approximations" portion which is Concept 7.

Unit G Summary Question #10: Range

While the domain of a rational function depends on DIVAH, what do you think the range of a rational function depends on? Give an example.

Because a hole is a point with a x and a y value, a hole would be an area where the range of a rational function is limited. A horizontal asymptote is an imaginary horizontal line so that means all the values on a horizontal asymptote is another limit to the range of a rational function.

Unit G Summary Question #9: X-intercept

Describe how to find the x-intercepts of a rational function. Include both the long way and the shortcut way, explaining why the shortcut makes mathematical sense.

To find the x-intercept, you have to plug in 0 for y in the factored equation, both the numerator and the denominator. That is the "long" way. The shortcut way would be just plugging in 0 for the numerator. This makes sense because if you plug in 0 for the denominator, the denominator will eventually cancel after it is multiplied to zero which is done to get the numerator by itself.

Unit G Summary Question #8: Y-intercept

How do you find the y-intercept of a rational function? Does this need to be done in the original or simplified equation?

To find the y-intercept of a rational function, simply plug in 0 for all the x's in the function. It should be done with the simplified equation but it is possible to do it with the original one.

Unit G Summary Question #7: Limit Notation for VAs

Describe how to write limit notation for vertical asymptotes and what the notation means.

To write limit notation for vertical asymptotes, a graphing calculator is required. The first part of the limit notation (as x-->_) has to do with what the equation/equations is/are. If the equation is x=2, then the x--> part will have 2. The second part needs a graphing calculator because it will tell you the function will be at the right or the left of the vertical asymptote and whether it will go up or down.

Unit G Summary Question #6: Holes

How do we find the appropriate place to plot a hole if the y-value is undefined when plugged into the original equation?

First one must need to know how to find a hole in order before I can go any further. You find the hole, which is a point, by plugging in the number you get for a vertical asymptote into the factored equation that has not been cancelled. You will get a value and that value will be the y-value of your hole. Now sometimes the y-value is undefined when a hole is plugged into the original equation. This will not matter because you are supposed to plug in the hole into the simplified/not cancelled equation which will give you a rational/real y-value as your answer.

Unit G Summary Question #5: Asymptote Exceptions

Describe the conditions in which a graph can cross through an asymptote.

It is true that graphs are not supposed to cross an asymptote, there is an exception to this as there is with a lot of rules in this world. Graphs can cross through an asymptote, specifically a horizontal or a slant one. A graph can cross through a horizontal one towards the far right or far left of the graph. A graph can cross through a slant one towards the middle of the graph. They will only cross through a graph slightly, however. It is impossible for a graph to cross a vertical asymptote.

Unit G Summary Question #4: Vertical Asymptotes and Holes

What is the difference between a graph having a vertical asymptote and a graph having a hole?

A graph that has a vertical asymptote means that a function can approach but never touch that vertical asymptote. A graph that has a hole means that a function will get close to it, skip it, and continue on as if it were there but you actually do not touch it. The image on the left shows a vertical asymptote as a red dashed line.The image on the right shows a few holes in the functions. The every unusual function with a numerator and denominator will have a vertical asymptote whereas a hole only exists if something cancels when factoring the function.

Unit G Summary Question 3: Slant Asymptotes

When does a graph have a slant asypmtote? How do you find the equation of the slant asymptote?

A slant asymptote is a diagonal imaginary line that a graph approaches but should not touch. A graph has a slant asymptote when the degree of the numerator is one, exactly one, degree bigger than the degree on the denominator of a function. What this means is that if the x (or whatever variable) on the top of a function has one power more than the the x on the bottom, the graph has a slant asymptote. To find the equation of the slant asymptote, one divide the numerator by the denominator using long division. The equation will be your answer excluding the remainder.

Unit G Summary Question #2: H.A. - Limit Notation

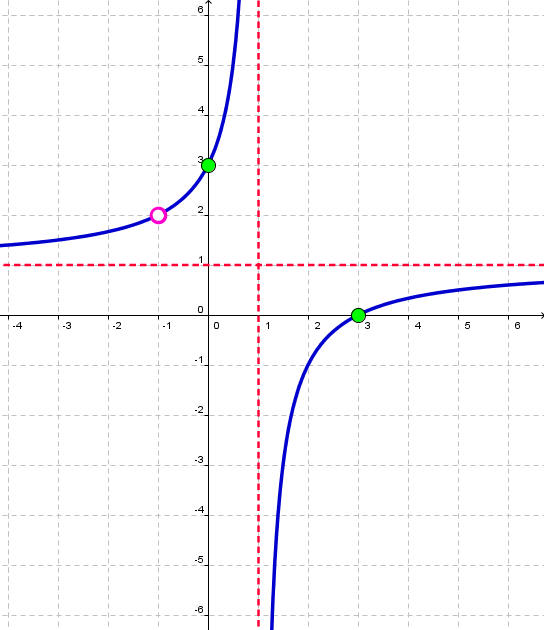
Describe what limit notation for horizontal asymptotes actually means.

Don't tell me what to do! Limit notation for horizontal asymptotes looks like this:
as x --> infinity, f(x) -->__
as x --> -infinity, f(x) -->__
In the case of that graph above, that line next to the arrow would be 0. This means that as a graph goes to the right, it will approach but not touch that number for a y-value and it would mean the same for when it goes to the left. The limit notation for horizontal asymptotes is just a fancy mathematical way of saying what boundaries a graph has like a soccer player cannot go out of bounds if he wants to keep possession of the ball.

Unit G Summary Question #1: Horizontal Asymptotes

How do we know if a graph has a horizontal asymptote? What are the three options?

To answer this question, first I feel the need to define what a horizontal asymptote is. A horizontal asymptote is an imaginary horizontal line that a graph cannot touch like in the example above where that curved line got close to but did not cross the y=4 horizontal asymptote. We know if a graph has a horizontal asymptote when we see that a graph approaches a y-value but never actually reaches it in a graphing calculator or in a graph in general. Another way we know if a graph has a horizontal asymptote is when you find that you get a bigger degree on the bottom (the denominator) after you compare the degrees of the numerator and the denominator of a function. The third way is when both the numerator and denominator of a function have the same degrees.